Números Decimais: O Que São, Exemplos, Operações – Mundo Educação introduz um tópico fundamental da matemática, explorando a natureza e o manuseio de números decimais. Compreender números decimais é crucial, pois eles permeiam diversas áreas do conhecimento e da vida cotidiana, desde cálculos financeiros até medições científicas. Esta análise aprofundará os conceitos, métodos operacionais e aplicações práticas desses números, fornecendo uma base sólida para o entendimento e a utilização eficiente em diferentes contextos.
A representação dos números decimais, seja na forma fracionária, decimal ou percentual, será detalhadamente examinada, juntamente com as técnicas para conversão entre essas formas. As operações aritméticas – adição, subtração, multiplicação e divisão – serão abordadas com exemplos práticos, destacando as similaridades e diferenças em relação às operações com números inteiros. Finalmente, serão apresentadas aplicações reais dos números decimais, ilustrando sua relevância em situações do dia a dia e em áreas como finanças e engenharia.
Conceito e Representação de Números Decimais: Números Decimais: O Que São, Exemplos, Operações – Mundo Educação

Números decimais são uma extensão do sistema de numeração decimal, permitindo a representação de quantidades menores que uma unidade. Sua importância na matemática é fundamental, pois eles permitem expressar frações de forma mais prática e realizar cálculos com maior precisão em diversas áreas, como física, engenharia, economia e ciências em geral. A capacidade de representar valores não inteiros é crucial para modelar e resolver problemas do mundo real.
Definição e Importância dos Números Decimais

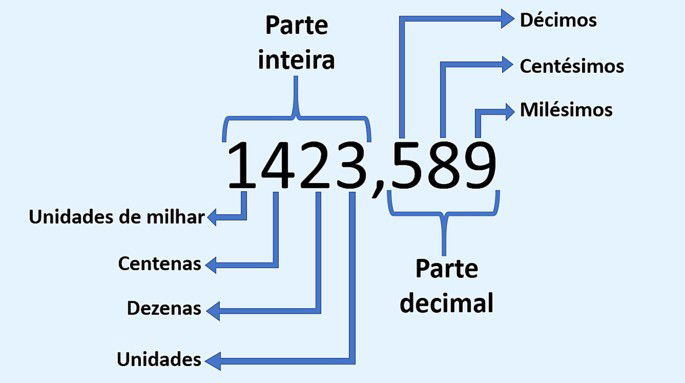
Números decimais são números que possuem uma parte inteira e uma parte decimal, separadas por uma vírgula (em português) ou um ponto (em inglês). A parte decimal representa frações de uma unidade, utilizando potências negativas de dez. A compreensão e o uso eficaz dos números decimais são essenciais para a resolução de problemas em diversas áreas do conhecimento, possibilitando cálculos mais precisos e uma representação mais completa de quantidades.
Eles são a base para muitas operações matemáticas avançadas e modelagem de fenômenos.
Formas de Representação de Números Decimais

Existem três formas principais de representar um número decimal: fracionária, decimal e percentual. A forma fracionária representa o número como uma razão entre dois números inteiros, enquanto a forma decimal utiliza a vírgula para separar a parte inteira da parte decimal. A forma percentual expressa o número como uma fração de 100. A escolha da representação depende do contexto e da necessidade de precisão.
Tabela de Exemplos de Números Decimais
A tabela a seguir ilustra exemplos de números decimais em suas diferentes representações, incluindo números positivos e negativos:
| Fracionário | Decimal | Percentual | Observações |
|---|---|---|---|
| 3/4 | 0,75 | 75% | Número decimal positivo |
| -1/2 | -0,5 | -50% | Número decimal negativo |
| 17/5 | 3,4 | 340% | Número decimal positivo maior que 1 |
| -2/100 | -0,02 | -2% | Número decimal negativo menor que 1 |
Conversão entre Frações e Números Decimais, Números Decimais: O Que São, Exemplos, Operações – Mundo Educação

A conversão de uma fração para um número decimal envolve a divisão do numerador pelo denominador. Por exemplo, para converter 3/4 em decimal, dividimos 3 por 4, resultando em 0,75.
Exemplo: 3/4 = 3 ÷ 4 = 0,75
A conversão de um número decimal para uma fração requer a identificação do valor posicional de cada dígito na parte decimal. Por exemplo, para converter 0,75 em fração, observamos que 0,75 representa 75 centésimos, ou seja, 75/100. Simplificando a fração, obtemos 3/4.
Exemplo: 0,75 = 75/100 = 3/4
Em resumo, o domínio dos números decimais é essencial para a compreensão e resolução de problemas em diversos campos. Este estudo demonstrou a importância da sua representação em diferentes formatos, a execução das operações aritméticas e a sua aplicação prática em contextos variados. A capacidade de converter frações em decimais e vice-versa, assim como a habilidade de realizar cálculos com precisão, são competências fundamentais para o sucesso em áreas que exigem raciocínio quantitativo.
A compreensão sólida desses conceitos abre portas para um aprendizado mais aprofundado em matemática e em outras disciplinas científicas e tecnológicas.

